澳门足球博彩网上投注

近日，澳門足球博彩網上投注-澳門足彩 教授朱家明，聯合清華大學高華健院士團隊、中科院力學所劉小明研究員團隊在《美國科澳門足球博彩網上投注 院刊》(PNAS)發表研究論文“Universal exact solutions for multiphysical inhomogeneities and inclusions in Fourier space”。該研究建立了廣義等效夾雜方程通用精確解，統一了單夾雜和多夾雜體系理論框架，建立了多物理復合材料平均模量精確解，提出了任意形狀裂紋應力強度因子通解。這項突破性工作解決了固體力學、固體物理和材料科學等多學科的長期難題。該研究得到了國家自然科學基金、山東省自然科學基金和廣東省自然科學基金等資助。

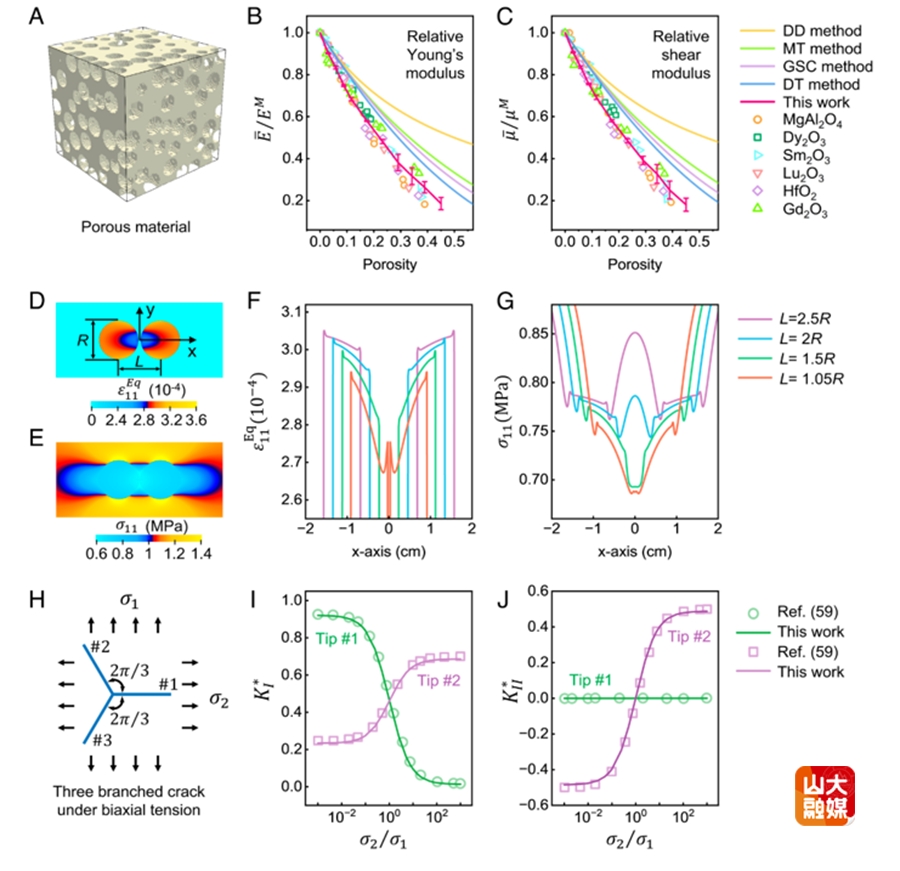
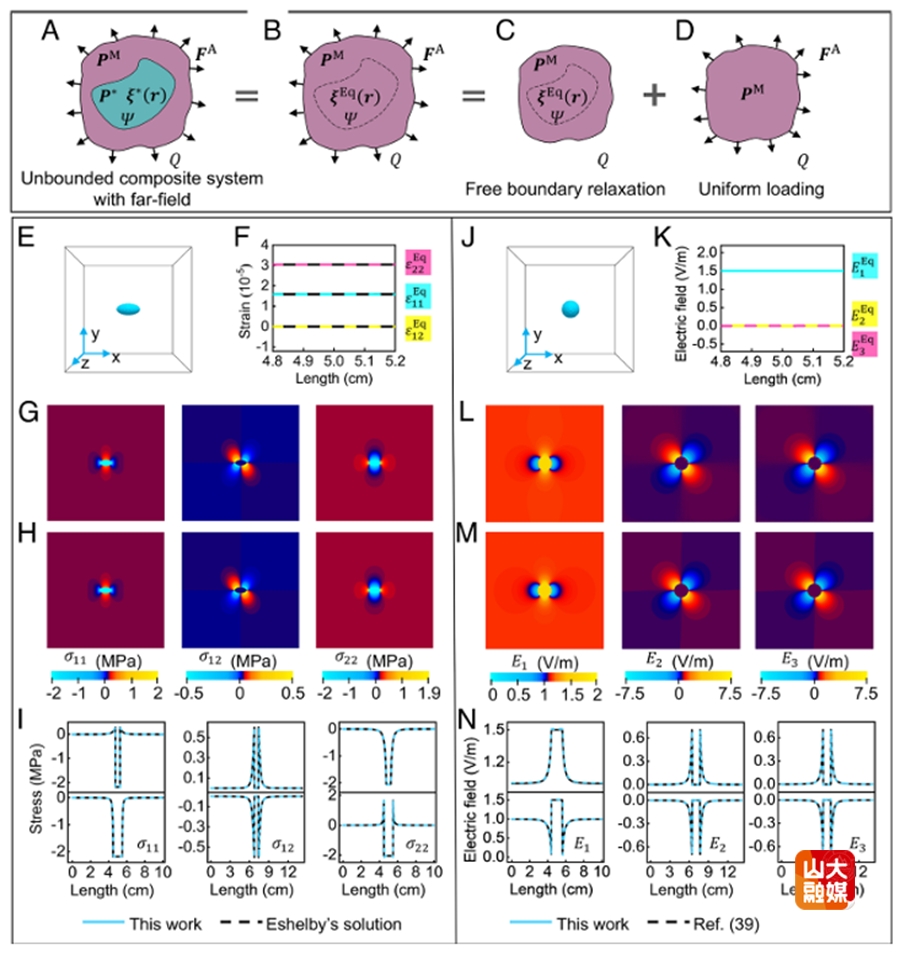
150多年來，關于異質夾雜如何影響材料宏觀物理性能一直是固體力學、物理學和材料科學的核心問題，麥克斯韋、瑞利和愛因斯坦對這一問題開展了影響深遠的研究。Eshelby的工作奠定了彈性夾雜理論的基礎，但僅能對簡單夾雜系統精確計算。關于任意異質夾雜體系的精確解這一難題至今仍懸而未決。為此，研究團隊通過求解廣義等效夾雜方程在傅氏空間建立了任意形狀、任意各向異性、任意異質夾雜的三維通用精確解，統一了單夾雜和多夾雜體系理論框架。通過這些精確解，研究團隊建立了多物理復合材料平均模量精確解，使均勻化理論進入精算時代；提出了任意形狀裂紋應力強度因子通解，為計算復雜裂紋應力強度因子提供了有效方法；建立了負泊松比材料設計準則；進一步驗證了特殊形狀夾雜的Eshelby猜想。

朱家明教授為本文第一作者和通訊作者。高華健院士、劉小明研究員為本文共同通訊作者。山東大學教授張慶松、張波，北京科技大學教授吳宏輝等參與該研究。

文：朱家明